A DSMC-PIC coupling method for the Vlasov-Maxwell-Landau system

Andrea Medaglia, Lorenzo Pareschi, Mattia Zanella (preprint arXiv:2510.22226, 2025)

We present a numerical framework for the simulation of collisional plasma dynamics, based on a coupling between Direct Simulation Monte Carlo (DSMC) and Particle-in-Cell (PIC) methods for the Vlasov-Maxwell-Landau system. The approach extends previously developed DSMC techniques for the homogeneous Landau equation to the fully inhomogeneous, electromagnetic regime. The Landau collision operator is treated through a stochastic particle formulation inspired by the grazing-collision limit of the Boltzmann equation, which enables an efficient and physically consistent representation of Coulomb interactions without relying on the full Boltzmann structure.

Augmented data and neural networks for robust epidemic forecasting: application to COVID-19 in Italy

Giacomo Dimarco, Federica Ferrarese, Lorenzo Pareschi (preprint arXiv:2510.09192)

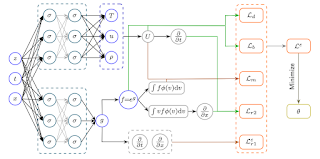
In this work, we propose a data augmentation strategy aimed at improving the training phase of neural networks and, consequently, the accuracy of their predictions. Our approach relies on generating synthetic data through a suitable compartmental model combined with the incorporation of uncertainty. The available data are then used to calibrate the model, which is further integrated with deep learning techniques to produce additional synthetic data for training. The results show that neural networks trained on these augmented datasets exhibit significantly improved predictive performance. We focus in particular on two different neural network architectures: Physics-Informed Neural Networks (PINNs) and Nonlinear Autoregressive (NAR) models.

Multi-Order Monte Carlo IMEX hierarchies for uncertainty quantification in multiscale hyperbolic systems

Giulia Bertaglia, Walter Boscheri, Lorenzo Pareschi (preprint arXiv:2508.20187)

We introduce a novel Multi-Order Monte Carlo approach for uncertainty quantification in the context of multiscale time-dependent partial differential equations. The new framework leverages Implicit-Explicit Runge-Kutta time integrators to satisfy the asymptotic-preserving property across different discretization orders of accuracy. In contrast to traditional Multi-Level Monte Carlo methods, which require costly hierarchical re-meshing, our method constructs a multi-order hierarchy by varying both spatial and temporal discretization orders within the Monte Carlo framework. This enables efficient variance reduction while naturally adapting to the multiple scales inherent in the problem.

Swarm-based optimization with jumps: a kinetic BGK framework and convergence analysis

 

Giacomo Borghi, Hyesung Im, Lorenzo Pareschi (preprint arXiv:2507.00871)

Metaheuristic algorithms are powerful tools for global optimization, particularly for non-convex and non-differentiable problems where exact methods are often impractical. Particle-based optimization methods, inspired by swarm intelligence principles, have shown effectiveness due to their ability to balance exploration and exploitation within the search space. In this work, we introduce a novel particle-based optimization algorithm where velocities are updated via random jumps, a strategy commonly used to enhance stochastic exploration.

Structure and asymptotic preserving deep neural surrogates for uncertainty quantification in multiscale kinetic equations

Wei Chen, Giacomo Dimarco, Lorenzo Pareschi (preprint arXiv:2506.10636)

The high dimensionality of kinetic equations with stochastic parameters poses major computational challenges for uncertainty quantification (UQ). Traditional Monte Carlo (MC) sampling methods, while widely used, suffer from slow convergence and high variance, which become increasingly severe as the dimensionality of the parameter space grows. To accelerate MC sampling, we adopt a multiscale control variates strategy that leverages low-fidelity solutions from simplified kinetic models to reduce variance.