Augmented data and neural networks for robust epidemic forecasting: application to COVID-19 in Italy

Giacomo Dimarco, Federica Ferrarese, Lorenzo Pareschi (preprint arXiv:2510.09192)

In this work, we propose a data augmentation strategy aimed at improving the training phase of neural networks and, consequently, the accuracy of their predictions. Our approach relies on generating synthetic data through a suitable compartmental model combined with the incorporation of uncertainty. The available data are then used to calibrate the model, which is further integrated with deep learning techniques to produce additional synthetic data for training. The results show that neural networks trained on these augmented datasets exhibit significantly improved predictive performance. We focus in particular on two different neural network architectures: Physics-Informed Neural Networks (PINNs) and Nonlinear Autoregressive (NAR) models.

Multi-Order Monte Carlo IMEX hierarchies for uncertainty quantification in multiscale hyperbolic systems

Giulia Bertaglia, Walter Boscheri, Lorenzo Pareschi (preprint arXiv:2508.20187)

We introduce a novel Multi-Order Monte Carlo approach for uncertainty quantification in the context of multiscale time-dependent partial differential equations. The new framework leverages Implicit-Explicit Runge-Kutta time integrators to satisfy the asymptotic-preserving property across different discretization orders of accuracy. In contrast to traditional Multi-Level Monte Carlo methods, which require costly hierarchical re-meshing, our method constructs a multi-order hierarchy by varying both spatial and temporal discretization orders within the Monte Carlo framework. This enables efficient variance reduction while naturally adapting to the multiple scales inherent in the problem.

Swarm-based optimization with jumps: a kinetic BGK framework and convergence analysis

 

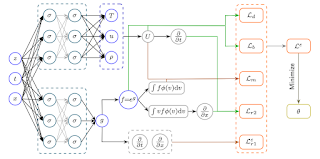
Giacomo Borghi, Hyesung Im, Lorenzo Pareschi (preprint arXiv:2507.00871)

Metaheuristic algorithms are powerful tools for global optimization, particularly for non-convex and non-differentiable problems where exact methods are often impractical. Particle-based optimization methods, inspired by swarm intelligence principles, have shown effectiveness due to their ability to balance exploration and exploitation within the search space. In this work, we introduce a novel particle-based optimization algorithm where velocities are updated via random jumps, a strategy commonly used to enhance stochastic exploration.

Structure and asymptotic preserving deep neural surrogates for uncertainty quantification in multiscale kinetic equations

Wei Chen, Giacomo Dimarco, Lorenzo Pareschi (preprint arXiv:2506.10636)

The high dimensionality of kinetic equations with stochastic parameters poses major computational challenges for uncertainty quantification (UQ). Traditional Monte Carlo (MC) sampling methods, while widely used, suffer from slow convergence and high variance, which become increasingly severe as the dimensionality of the parameter space grows. To accelerate MC sampling, we adopt a multiscale control variates strategy that leverages low-fidelity solutions from simplified kinetic models to reduce variance.

Superlinear Drift in Consensus-Based Optimization with Condensation Phenomena

Jonathan Franceschi, Lorenzo Pareschi, Mattia Zanella (preprint arXiv:2506.09001)

Consensus-based optimization (CBO) is a class of metaheuristic algorithms designed for global optimization problems. In the many-particle limit, classical CBO dynamics can be rigorously connected to mean-field equations that ensure convergence toward global minimizers under suitable conditions. In this work, we draw inspiration from recent extensions of the Kaniadakis--Quarati model for indistinguishable bosons to develop a novel CBO method governed by a system of SDEs with superlinear drift and nonconstant diffusion. The resulting mean-field formulation in one dimension exhibits condensation-like phenomena, including finite-time blow-up and loss of L2-regularity.